Регрессионный анализ как метод статистического анализа

Регрессионный анализ — статистический метод исследования зависимости случайной величины от переменных

В статистическом моделировании регрессионный анализ представляет собой исследования, применяемые с целью оценки взаимосвязи между переменными. Этот математический метод включает в себя множество других методов для моделирования и анализа нескольких переменных, когда основное внимание уделяется взаимосвязи между зависимой переменной и одной или несколькими независимыми. Говоря более конкретно, регрессионный анализ помогает понять, как меняется типичное значение зависимой переменной, если одна из независимых переменных изменяется, в то время как другие независимые переменные остаются фиксированными.

Во всех случаях целевая оценка является функцией независимых переменных и называется функцией регрессии. В регрессионном анализе также представляет интерес характеристика изменения зависимой переменной как функции регрессии, которая может быть описана с помощью распределения вероятностей.

Данный статистический метод исследования широко используется для прогнозирования, где его использование имеет существенное преимущество, но иногда это может приводить к иллюзии или ложным отношениям, поэтому рекомендуется аккуратно его использовать в указанном вопросе, поскольку, например, корреляция не означает причинно-следственной связи.

Разработано большое число методов для проведения регрессионного анализа, такие как линейная и обычная регрессии по методу наименьших квадратов, которые являются параметрическими. Их суть в том, что функция регрессии определяется в терминах конечного числа неизвестных параметров, которые оцениваются из данных. Непараметрическая регрессия позволяет ее функции лежать в определенном наборе функций, которые могут быть бесконечномерными.

Как статистический метод исследования, регрессионный анализ на практике зависит от формы процесса генерации данных и от того, как он относится к регрессионному подходу. Так как истинная форма процесса данных, генерирующих, как правило, неизвестное число, регрессионный анализ данных часто зависит в некоторой степени от предположений об этом процессе. Эти предположения иногда проверяемы, если имеется достаточное количество доступных данных. Регрессионные модели часто бывают полезны даже тогда, когда предположения умеренно нарушены, хотя они не могут работать с максимальной эффективностью.

В более узком смысле регрессия может относиться конкретно к оценке непрерывных переменных отклика, в отличие от дискретных переменных отклика, используемых в классификации. Случай непрерывной выходной переменной также называют метрической регрессией, чтобы отличить его от связанных с этим проблем.

Самая ранняя форма регрессии — это всем известный метод наименьших квадратов. Он был опубликован Лежандром в 1805 году и Гауссом в 1809. Лежандр и Гаусс применили метод к задаче определения из астрономических наблюдений орбиты тел вокруг Солнца (в основном кометы, но позже и вновь открытые малые планеты). Гаусс опубликовал дальнейшее развитие теории наименьших квадратов в 1821 году, включая вариант теоремы Гаусса-Маркова.

Термин «регресс» придумал Фрэнсис Гальтон в XIX веке, чтобы описать биологическое явление. Суть была в том, что рост потомков от роста предков, как правило, регрессирует вниз к нормальному среднему. Для Гальтона регрессия имела только этот биологический смысл, но позже его работа была продолжена Удни Йолей и Карлом Пирсоном и выведена к более общему статистическому контексту. В работе Йоля и Пирсона совместное распределение переменных отклика и пояснительных считается гауссовым. Это предположение было отвергнуто Фишером в работах 1922 и 1925 годов. Фишер предположил, что условное распределение переменной отклика является гауссовым, но совместное распределение не должны быть таковым. В связи с этим предположение Фишера ближе к формулировке Гаусса 1821 года. До 1970 года иногда уходило до 24 часов, чтобы получить результат регрессионного анализа.

Методы регрессионного анализа продолжают оставаться областью активных исследований. В последние десятилетия новые методы были разработаны для надежной регрессии; регрессии с участием коррелирующих откликов; методы регрессии, вмещающие различные типы недостающих данных; непараметрической регрессии; байесовские методов регрессии; регрессии, в которых переменные прогнозирующих измеряются с ошибкой; регрессии с большей частью предикторов, чем наблюдений, а также причинно-следственных умозаключений с регрессией.

Модели регрессионного анализа включают следующие переменные:

• Неизвестные параметры, обозначенные как бета, которые могут представлять собой скаляр или вектор.
• Независимые переменные, X.
• Зависимые переменные, Y.

В различных областях науки, где осуществляется применение регрессионного анализа, используются различные термины вместо зависимых и независимых переменных, но во всех случаях регрессионная модель относит Y к функции X и β.

Приближение обычно оформляется в виде E (Y | X) = F (X, β). Для проведения регрессионного анализа должен быть определен вид функции f. Реже она основана на знаниях о взаимосвязи между Y и X, которые не полагаются на данные. Если такое знание недоступно, то выбрана гибкая или удобная форма F.

Предположим теперь, что вектор неизвестных параметров β имеет длину k. Для выполнения регрессионного анализа пользователь должен предоставить информацию о зависимой переменной Y:

• Если наблюдаются точки N данных вида (Y, X), где N точки к данным. В этом случае имеется достаточно информации в данных, чтобы оценить уникальное значение для β, которое наилучшим образом соответствует данным, и модель регрессии, когда применение к данным можно рассматривать как переопределенную систему в β.

В последнем случае регрессионный анализ предоставляет инструменты для:

• Поиска решения для неизвестных параметров β, которые будут, например, минимизировать расстояние между измеренным и предсказанным значением Y.
• При определенных статистических предположениях, регрессионный анализ использует избыток информации для предоставления статистической информации о неизвестных параметрах β и предсказанные значения зависимой переменной Y.

Рассмотрим модель регрессии, которая имеет три неизвестных параметра: β, β₁ и β₂. Предположим, что экспериментатор выполняет 10 измерений в одном и том же значении независимой переменной вектора X. В этом случае регрессионный анализ не дает уникальный набор значений. Лучшее, что можно сделать, оценить среднее значение и стандартное отклонение зависимой переменной Y. Аналогичным образом измеряя два различных значениях X, можно получить достаточно данных для регрессии с двумя неизвестными, но не для трех и более неизвестных.

Если измерения экспериментатора проводились при трех различных значениях независимой переменной вектора X, то регрессионный анализ обеспечит уникальный набор оценок для трех неизвестных параметров в β.

В случае общей линейной регрессии приведенное выше утверждение эквивалентно требованию, что матрица X Т X обратима.

Когда число измерений N больше, чем число неизвестных параметров k и погрешности измерений ε_i, то, как правило, распространяется затем избыток информации, содержащейся в измерениях, и используется для статистических прогнозов относительно неизвестных параметров. Этот избыток информации называется степенью свободы регрессии.

Классические предположения для регрессионного анализа включают в себя:

• Выборка является представителем прогнозирования логического вывода.
• Ошибка является случайной величиной со средним значением нуля, который является условным на объясняющих переменных.
• Независимые переменные измеряются без ошибок.
• В качестве независимых переменных (предикторов) они линейно независимы, то есть не представляется возможным выразить любой предсказатель в виде линейной комбинации остальных.
• Ошибки являются некоррелированными, то есть ковариационная матрица ошибок диагоналей и каждый ненулевой элемент являются дисперсией ошибки.
• Дисперсия ошибки постоянна по наблюдениям (гомоскедастичности). Если нет, то можно использовать метод взвешенных наименьших квадратов или другие методы.

Эти достаточные условия для оценки наименьших квадратов обладают требуемыми свойствами, в частности эти предположения означают, что оценки параметров будут объективными, последовательными и эффективными, в особенности при их учете в классе линейных оценок. Важно отметить, что фактические данные редко удовлетворяют условиям. То есть метод используется, даже если предположения не верны. Вариация из предположений иногда может быть использована в качестве меры, показывающей, насколько эта модель является полезной. Многие из этих допущений могут быть смягчены в более продвинутых методах. Отчеты статистического анализа, как правило, включают в себя анализ тестов по данным выборки и методологии для полезности модели.

Кроме того, переменные в некоторых случаях ссылаются на значения, измеренные в точечных местах. Там могут быть пространственные тенденции и пространственные автокорреляции в переменных, нарушающие статистические предположения. Географическая взвешенная регрессия — единственный метод, который имеет дело с такими данными.

В линейной регрессии особенностью является то, что зависимая переменная, которой является Y_i, представляет собой линейную комбинацию параметров. Например, в простой линейной регрессии для моделирования n-точек используется одна независимая переменная, x_i, и два параметра, β и β₁.

При множественной линейной регрессии существует несколько независимых переменных или их функций.

При случайной выборке из популяции ее параметры позволяют получить образец модели линейной регрессии.

В данном аспекте популярнейшим является метод наименьших квадратов. С помощью него получают оценки параметров, которые минимизируют сумму квадратов остатков. Такого рода минимизация (что характерно именно линейной регрессии) этой функции приводит к набору нормальных уравнений и набору линейных уравнений с параметрами, которые решаются с получением оценок параметров.

При дальнейшем предположении, что ошибка популяции обычно распространяется, исследователь может использовать эти оценки стандартных ошибок для создания доверительных интервалов и проведения проверки гипотез о ее параметрах.

Пример, когда функция не является линейной относительно параметров, указывает на то, что сумма квадратов должна быть сведена к минимуму с помощью итерационной процедуры. Это вносит много осложнений, которые определяют различия между линейными и нелинейными методами наименьших квадратов. Следовательно, и результаты регрессионного анализа при использовании нелинейного метода порой непредсказуемы.

Здесь, как правило, нет согласованных методов, касающихся числа наблюдений по сравнению с числом независимых переменных в модели. Первое правило было предложено Доброй и Хардином и выглядит как N = t^n, где N является размер выборки, n — число независимых переменных, а t есть числом наблюдений, необходимых для достижения желаемой точности, если модель имела только одну независимую переменную. Например, исследователь строит модель линейной регрессии с использованием набора данных, который содержит 1000 пациентов (N). Если исследователь решает, что необходимо пять наблюдений, чтобы точно определить прямую (м), то максимальное число независимых переменных, которые модель может поддерживать, равно 4.

Несмотря на то что параметры регрессионной модели, как правило, оцениваются с использованием метода наименьших квадратов, существуют и другие методы, которые используются гораздо реже. К примеру, это следующие методы:

• Байесовские методы (например, байесовский метод линейной регрессии).
• Процентная регрессия, использующаяся для ситуаций, когда снижение процентных ошибок считается более целесообразным.
• Наименьшие абсолютные отклонения, что является более устойчивым в присутствии выбросов, приводящих к квантильной регрессии.
• Непараметрическая регрессия, требующая большого количества наблюдений и вычислений.
• Расстояние метрики обучения, которая изучается в поисках значимого расстояния метрики в заданном входном пространстве.

Все основные статистические пакеты программного обеспечения выполняются с помощью наименьших квадратов регрессионного анализа. Простая линейная регрессия и множественный регрессионный анализ могут быть использованы в некоторых приложениях электронных таблиц, а также на некоторых калькуляторах. Хотя многие статистические пакеты программного обеспечения могут выполнять различные типы непараметрической и надежной регрессии, эти методы менее стандартизированы; различные программные пакеты реализуют различные методы. Специализированное регрессионное программное обеспечение было разработано для использования в таких областях как анализ обследования и нейровизуализации.

источник

Регрессионный анализ — это метод установления аналитического выражения стохастической зависимости между исследуемыми признаками. Уравнение регрессии показывает, как в среднем изменяется у при изменении любого из x_i, и имеет вид:

где у — зависимая переменная (она всегда одна);

х_i— независимые переменные (факторы) (их может быть несколько).

Если независимая переменная одна — это простой регрессионный анализ. Если же их несколько (п 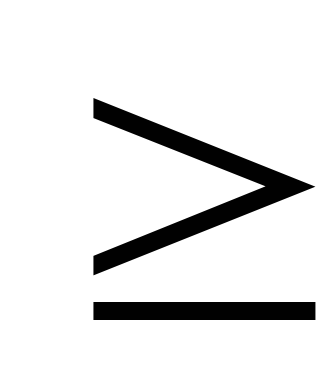2), то такой анализ называется многофакторным.

В ходе регрессионного анализа решаются две основные задачи:

построение уравнения регрессии, т.е. нахождение вида зависимости между результатным показателем и независимыми факторами x₁, x₂, …, x_n.

оценка значимости полученного уравнения, т.е. определение того, насколько выбранные факторные признаки объясняют вариацию признака у.

Применяется регрессионный анализ главным образом для планирования, а также для разработки нормативной базы.

В отличие от корреляционного анализа, который только отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. Кроме того, если корреляционный анализ изучает любую взаимосвязь факторов, то регрессионный — одностороннюю зависимость, т.е. связь, показывающую, каким образом изменение факторных признаков влияет на признак результативный.

Регрессионный анализ — один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, x_l,x₂. x_n; y должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида:

Построение уравнения регрессии осуществляется, как правило, методом наименьших квадратов, суть которого состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

j = a + b₁x₁j + b₂x₂j + . + b_nх_nj — расчетное значение результатного фактора.

Коэффициенты регрессии рекомендуется определять с помощью аналитических пакетов для персонального компьютера или специального финансового калькулятора. В наиболее простом случае коэффициенты регрессии однофакторного линейного уравнения регрессии вида y = а + bх можно найти по формулам:

Кластерный анализ — один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующееся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве. Расстояние между точками р и q с k координатами определяется как:

Основным критерием кластеризации является то, что различия между кластерами должны быть более существенны, чем между наблюдениями, отнесенными к одному кластеру, т.е. в многомерном пространстве должно соблюдаться неравенство:

где r_1,2 — расстояние между кластерами 1 и 2.

Так же как и процедуры регрессионного анализа, процедура кластеризации достаточно трудоемка, ее целесообразно выполнять на компьютере.

источник

Корреляционно-регрессионный анализ — один из наиболее широко распространенных и гибких приемов обработки стати­стических данных. Данный метод начинает свой отсчет с 1795 г., когда английский исследователь Фрэнсис Гальтон предложил теоретические основы регрессионного метода, а в 1801 г. рассчи­тал с его помощью траекторию полета планеты Церера. Им же введен в статистику термин «корреляция». Можно также назвать

французского кристаллографа Огюста Браве, немецкого физика Густава Теодора Фехнера, английского экономиста и статистика Фрэнсиса Эджуорта, впервые высказывавших в середине—конце XIX в. идеи о количественном измерении связей явлений. В раз­ное время над теорией анализа работали известные в области теоретической статистики ученые Карл Фридрих Гаусс (Герма­ния), Адриен Мари Лежандр (Франция), Карл Пирсон (Англия) и др.

Корреляционно-регрессионный анализ состоит в построении и анализе экономико-математической модели в виде уравнения регрессии (корреляционной связи), характеризующего зависи­мость признака от определяющих его факторов.

Корреляционно-регрессионный анализ предполагает сле­дующие этапы:

• предварительный анализ (здесь формулируются основные направления всего анализа, определяется методика оценки ре­зультативного показателя и перечень наиболее существенных факторов);

• сбор информации и ее первичная обработка;

• построение модели (один из важнейших этапов);

Задачи корреляционного анализа сводятся к выделению важ­нейших факторов, которые влияют на результативный признак, измерению тесноты связи между факторами, выявлению неиз­вестных причин связей и оценке факторов, оказывающих макси­мальное влияние на результат.

Задачи регрессионного анализа заключаются в установлении формы зависимости, определении уравнения регрессии и его ис­пользовании для оценки неизвестных значений зависимой пере­менной, прогнозировании возможных значений результативного признака при задаваемых значениях факторных признаков.

При использовании корреляционно-регрессионного анализа необходимо соблюдать следующие требования.

1. Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.

2. Все факторные признаки должны иметь количественное (цифровое) выражение.

3. Необходимо наличие массовости значений изучаемых по­казателей.

4. Причинно-следственные связи между явлениями и процес­сами могут быть описаны линейной или приводимой к линейной формой зависимости.

5. Не должно быть количественных ограничений на парамет­ры модели связи.

6. Необходимо обеспечить постоянство территориальной и временной структуры изучаемой совокупности.

Корреляция — статистическая зависимость между случай­ными величинами, не имеющими строго функционального харак­тера, при которой изменение одной из случайных величин приво­дит к изменению математического ожидания другой.

В статистике принято различать следующие варианты зави­симостей.

1. Парная корреляция — связь между двумя признаками (ре­зультативным и факторным).

2. Частная корреляция — зависимость между результатив­ным и одним из факторных признаков при фиксированном значе­нии других факторных признаков.

3. Множественная корреляция — зависимость результатив­ного и двух или более факторных признаков, включенных в ис­следование.

Корреляционная связь — частный случай стохастической связи и состоит в том, что разным значениям одной переменной соответствуют различные средние значения другой.

Обязательное условие применения корреляционного метода — массовость значений изучаемых показателей, что позволяет вы­явить тенденцию, закономерность развития, форму взаимосвязи между признаками. Тогда, в соответствии с законом больших, чи­сел, влияние других факторов сглаживается, нейтрализуется. На­личие корреляционной связи присуще многим общественным явлениям.

Показатели тесноты связи между признаками называют ко­эффициентами корреляции. Их выбор зависит от того, в каких шкалах измерены признаки. Основными шкалами являются:

1) номинальная шкала (наименований) предназначена для описания принадлежности объектов к определенным социальным группам (например, коэффициенты ассоциации и контингенции, коэффициенты Пирсона и Чупрова);

2) шкала порядка (ординальная) применяется для измерения упорядоченности объектов по одному или нескольким признакам (например, коэффициенты Спирмена и Кенделла);

3) количественная шкала используется для описания количе­ственных показателей — например, линейный коэффициент кор­реляции и корреляционное отношение.

Корреляционный анализ — метод статистического исследо­вания экспериментальных данных, позволяющий определить сте­пень линейной зависимости между переменными.

Парная линейная корреляция — простейшая система корре­ляционной связи, представляющая линейную связь между двумя признаками. Ее практическое значение состоит в выделении од­ного важнейшего фактора, который и определяет вариацию ре­зультативного признака.

Для определения степени тесноты парной линейной зависи­мости служит линейный коэффициент корреляции, который был впервые введен в начале 1890-х гг. Пирсоном, Эджуортом и Велдоном. В теории разработаны и на практике применяются раз­личные варианты формул расчета данного коэффициента:

, где ,

При малом числе наблюдений для практических вычислений линейный коэффициент корреляции удобнее исчислять по формуле:

,

где r принимает значения в пределах от -1 до 1.

Чем ближе линейный коэффициент корреляции по абсолют­ной величине к I, тем теснее связь. С другой стороны, если он ра­вен 1, то зависимость является не стохастической, а функциональ­ной. Знак при нем указывает направление связи: знак «-» соответ­ствует обратной зависимости, «+» — прямой. Величина коэффициента корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям.

Степень взаимного влияния факторов в зависимости от ко­эффициента корреляции приведена в табл. 1.

Количественная оценка тесноты связи

при различных значениях коэффициента корреляции

После того, как с помощью корреляционного анализа выяв­лено наличие статистических связей между переменными и оце­нена степень их тесноты, обычно переходят к математическому описанию зависимостей, то есть к регрессионному анализу.

Термин «регрессия» (произошел от латинского regression — отступление, возврат к чему-либо) был также введен Ф. Гальтоном в 1886 г. Обрабатывая статистические данные в связи с ана­лизом наследственности роста, он отметил прямую зависимость между ростом родителей и их детей (наблюдение само по себе не слишком глубокое). Но относительно старших сыновей ему уда­лось установить более тонкую зависимость. Он рассчитал, что средний рост старшего сына лежит между средним ростом насе­ления и средним ростом родителей. Если рост родителей выше среднего, то их наследник, как правило, ниже; если средний рост родителей ниже среднего, то рост их потомка выше. Когда Гальтон нанес на график средний рост старших сыновей для различ­ных значений среднего роста родителей, он получил почти пря­мую линию, проходящую через нанесенные точки.

Поскольку рост потомства стремится двигаться к среднему, Гальтон назвал это явление регрессией к среднему состоянию, а ли­нию, проходящую через точки на графике, — линией регрессии.

Регрессивный анализ применяется в тех случаях, когда необ­ходимо отыскать непосредственно вид зависимости х и у. При этом предполагается, что независимые факторы не случайные величины, а результативный показатель у имеет постоянную, не­зависимую от факторов дисперсию и стандартное отклонение.

Одна из проблем построения уравнения регрессии — размер­ность, то есть определение числа факторных признаков, вклю­чаемых в модель. Их число должно быть оптимальным.

Сокращение размерности за счет исключения второстепен­ных, несущественных факторов позволяет получить модель, бы­стрее и качественнее реализуемую. В то же время построение мо­дели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс в единой системе национального счетоводства.

При построении модели число факторных признаков должно быть в 5-6 раз меньше объема изучаемой совокупности.

Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависи­мость является линейной и выражается уравнением прямой.

Линейная регрессия сводится к нахождению уравнения вида:

где х — индивидуальное значение факторного признака; а, а₁ — параметры уравнения прямой (уравнения регрессии); у_х — теоре­тическое значение результирующего фактора.

Данное уравнение показывает среднее значение изменения ре­зультативного признака х на одну единицу его измерения. Знак па­раметра показывает направление этого изменения. На практике по­строение линейной регрессии сводится к оценке ее параметров а, а_1.

При классическом подходе параметры уравнения а, а₁ нахо­дятся методом наименьших квадратов, который позволяет полу­чить такие оценки параметров, при которых сумма квадратов от­клонений фактических значений результативного признака у от расчетных, теоретических (у_х) была бы минимальной.

Для нахождения минимума данной функции приравняем к нулю частные производные и тем самым получим систему двух линейных уравнений, которая называется системой нормальных уравнений:

В уравнении прямой параметр а экономического смысла не имеет, параметр а₁ является коэффициентом регрессии и показы­вает изменение результативного признака при изменении фак­торного на единицу.

Или по следующим формулам:

, где , , ,

Между линейным коэффициентом корреляции и коэффици­ентом регрессии существует определенная зависимость, выра­женная формулой

Часто исследуемые признаки имеют разные единицы измере­ния, поэтому для оценки влияния факторного признака на ре­зультативный применяется коэффициент эластичности. Он рас­считывается для каждой точки и в среднем по всей совокупности по формуле:

где у’_х — первая производная уравнения регрессии.

Коэффициент эластичности показывает, на сколько процен­тов изменяется результативный признак при изменении фактор­ного признака на 1%.

Чтобы иметь возможность судить о сравнительной связи влияния отдельных факторов и о тех резервах, которые в них за­ложены, должны быть вычислены частные (средние) коэффициенты эластичности.

Различия в единицах измерения факторов устраняют с помо­щью частных (средних) коэффициентов эластичности, которые рассчитываются по формуле:

где а_i — коэффициент регрессии при факторе х; — средние значения факторного и результативного признаков.

Частные коэффициенты эластичности показывают, на сколь­ко процентов в среднем изменяется анализируемый показатель с изменением на 1 % каждого фактора при фиксированном поло­жении других факторов.

Альтернативным показателем степени зависимости между двумя переменными является линейный коэффициент детерми­нации, представляющий собой квадрат линейного коэффициента корреляции r 2 . Его числовое значение всегда заключено в пределе от 0 до 1. Он характеризует долю вариации (разброса) зависимой переменной. Значение коэффициента детерминации непосредст­венно указывает степень влияния независимого фактора на ре­зультативный показатель.

Степень тесноты связи полностью соответствует теоретиче­скому корреляционному отношению, которое является универ­сальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.

С помощью теоретического корреляционного отношения из­меряется теснота связи любой формы, а посредством линейного коэффициента корреляции — только прямолинейной связи.

Теоретическое корреляционное отношение рассчитывается по формулам:

где — факторная дисперсия; — общая дисперсия.

Для упрощения расчетов меры тесноты корреляционной свя­зи часто применятся индекс корреляционной связи, который оп­ределяется по формулам:

где — остаточная дисперсия.

Линейные модели отличаются простой интерпретируемостью и хорошо разработанными приемами оценивания коэффициентов регрессии. Обычно для них все три наиболее распространенных метода статистического оценивания — максимального правдопо­добия, наименьших квадратов и моментов — дают оптимальные решения и соответственно приводят к оценкам, обладающим ли­нейностью, эффективностью, несмещенностью. Принимая во внимание, что линейные регрессионные модели не могут с оди­наково высокой степенью достоверности описывать многообраз­ные процессы, происходящие в реальности, их дополняет боль­шой класс нелинейных моделей. Для последних, однако, с учетом их сложности и специфичности приемов параметрического оце­нивания предпочтительным остается приведение к простой ли­нейной форме.

источник

Деятельность людей во множестве случаев предполагает работу с данными, а она в свою очередь может подразумевать не только оперирование ими, но и их изучение, обработку и анализ. Например, когда нужно уплотнить информацию, найти какие-то взаимосвязи или определить структуры. И как раз для аналитики в этом случае очень удобно пользоваться не только разными техниками мышления, но и применять статистические методы.

Особенностью методов статистического анализа является их комплексность, обусловленная многообразием форм статистических закономерностей, а также сложностью процесса статистических исследований. Однако мы хотим поговорить именно о таких методах, которые может применять каждый, причем делать это эффективно и с удовольствием.

Статистическое исследование может проводиться посредством следующих методик:

• Статистическое наблюдение;
• Сводка и группировка материалов статистического наблюдения;
• Абсолютные и относительные статистические величины;
• Вариационные ряды;
• Выборка;
• Корреляционный и регрессионный анализ;
• Ряды динамики.

Далее мы рассмотрим каждый из них более подробно. Но отметим, что представим лишь основные характеристики без подробного описания алгоритмов действий. Впрочем, понять их не составит никакого труда.

Статистическое наблюдение является планомерным, организованным и в большинстве случаев систематическим сбором информации, направленным, главным образом, на явления социальной жизни. Реализуется данный метод через регистрацию предварительно определенных наиболее ярких признаков, цель которой состоит в последующем получении характеристик изучаемых явлений.

Статистическое наблюдение должно выполняться с учетом некоторых важных требований:

• Оно должно полностью охватывать изучаемые явления;
• Получаемые данные должны быть точными и достоверными;
• Получаемые данные должны быть однообразными и легкосопоставимыми.

Также статистическое наблюдение может иметь две формы:

• Отчетность – это такая форма статистического наблюдения, где информация поступает в конкретные статистические подразделения организаций, учреждений или предприятий. В этом случае данные вносятся в специальные отчеты.
• Специально организованное наблюдение – наблюдение, которое организуется с определенной целью, чтобы получить сведения, которых не имеется в отчетах, или же для уточнения и установления достоверности информации отчетов. К этой форме относятся опросы (например, опросы мнений людей), перепись населения и т.п.

Кроме того, статистическое наблюдение может быть категоризировано на основе двух признаков: либо на основе характера регистрации данных, либо на основе охвата единиц наблюдения. К первой категории относятся опросы, документирование и прямое наблюдение, а ко второй – наблюдение сплошное и несплошное, т.е. выборочное.

Для получения данных при помощи статистического наблюдения можно применять такие способы как анкетирование, корреспондентская деятельность, самоисчисление (когда наблюдаемые, например, сами заполняют соответствующие документы), экспедиции и составление отчетов.

Говоря о втором методе, в первую очередь следует сказать о сводке. Сводка представляет собой процесс обработки определенных единичных фактов, которые образуют общую совокупность данных, собранных при наблюдении. Если сводка проводится грамотно, огромное количество единичных данных об отдельных объектах наблюдения может превратиться в целый комплекс статистических таблиц и результатов. Также такое исследование способствует определению общих черт и закономерностей исследуемых явлений.

С учетом показателей точности и глубины изучения можно выделить простую и сложную сводку, но любая из них должна основываться на конкретных этапах:

• Выбирается группировочный признак;
• Определяется порядок формирования групп;
• Разрабатывается система показателей, позволяющих охарактеризовать группу и объект или явление в целом;
• Разрабатываются макеты таблиц, где будут представлены результаты сводки.

Важно заметить, что есть и разные формы сводки:

• Централизованная сводка, требующая передачи полученного первичного материала в вышестоящий центр для последующей обработки;
• Децентрализованная сводка, где изучение данных происходит на нескольких ступенях по восходящей.

Выполняться же сводка может при помощи специализированного оборудования, например, с использованием компьютерного ПО или вручную.

Что же касается группировки, то этот процесс отличается разделением исследуемых данных на группы по признакам. Особенности поставленных статистическим анализом задач влияют на то, какой именно будет группировка: типологической, структурной или аналитической. Именно поэтому для сводки и группировки либо прибегают к услугам узкопрофильных специалистов, либо применяют конкретные техники мышления.

Абсолютные величина считаются самой первой формой представления статистических данных. С ее помощью удается придать явлениям размерные характеристики, например, по времени, по протяженности, по объему, по площади, по массе и т.д.

Если требуется узнать об индивидуальных абсолютных статистических величинах, можно прибегнуть к замерам, оценке, подсчету или взвешиванию. А если нужно получить итоговые объемные показатели, следует использовать сводку и группировку. Нужно иметь в виду, что абсолютные статистические величины отличаются наличием единиц измерения. К таким единицам относят стоимостные, трудовые и натуральные.

А относительные величины выражают количественные соотношения, касающиеся явлений социальной жизни. Чтобы их получить, одни величины всегда делятся на другие. Показатель, с которым сравнивают (это знаменатель), называют основанием сравнения, а показатель, которой сравнивают (это числитель), называют отчетной величиной.

Относительные величины могут быть разными, что зависит от их содержательной части. Например, существуют величины сравнения, величины уровня развития, величины интенсивности конкретного процесса, величины координации, структуры, динамики и т.д. и т.п.

Чтобы изучить какую-то совокупность по дифференцирующимся признакам, в статистическом анализе применяются средние величины – обобщающие качественные характеристики совокупности однородных явлений по какому-либо дифференцирующемуся признаку.

Крайне важным свойством средних величин является то, что они говорят о значениях конкретных признаков во всем их комплексе единым числом. Невзирая на то, что у отдельных единиц может наблюдаться количественная разница, средние величины выражают общие значения, свойственные всем единицам исследуемого комплекса. Получается, что при помощи характеристики чего-то одного можно получить характеристику целого.

Следует иметь в виду, что одним из самых важных условий применения средних величин, если проводится статистический анализ социальных явлений, считается однородность их комплекса, для которого и нужно узнать среднюю величину. А от такого, как именно будут представлены начальные данные для исчисления средней величины, будет зависеть и формула ее определения.

В некоторых случаях данных о средних показателях тех или иных изучаемых величин может быть недостаточно, чтобы провести обработку, оценку и глубокий анализ какого-то явления или процесса. Тогда во внимание следует брать вариацию или разброс показателей отдельных единиц, который тоже представляет собой важную характеристику исследуемой совокупности.

На индивидуальные значения величин могут воздействовать многие факторы, а сами изучаемые явления или процессы могут быть очень многообразны, т.е. обладать вариацией (это многообразие и есть вариационные ряды), причины которой следует искать в сущности того, что изучается.

Вышеназванные абсолютные величины находятся в непосредственной зависимости от единиц измерения признаков, а значит, делают процесс изучения, оценки и сравнения двух и более вариационных рядов более сложным. А относительные показатели нужно вычислять в качестве соотношения абсолютных и средних показателей.

Смысл выборочного метода (или проще – выборки) состоит в том, что по свойствам одной части определяются численные характеристики целого (это называется генеральной совокупностью). Основной выборочного метода является внутренняя связь, объединяющая части и целое, единичное и общее.

Метод выборки отличается рядом существенных преимуществ перед остальными, т.к. благодаря уменьшению количества наблюдений позволяет сократить объемы работы, затрачиваемые средства и усилия, а также успешно получать данные о таких процессах и явлениях, где либо нецелесообразно, либо просто невозможно исследовать их полностью.

Соответствие характеристик выборки характеристикам изучаемого явления или процесса будет зависеть от комплекса условий, и в первую очередь от того, как вообще будет реализовываться выборочный метод на практике. Это может быть как планомерный отбор, идущий по подготовленной схеме, так и непланомерный, когда выборка производится из генеральной совокупности.

Но во всех случаях выборочный метод должен быть типичным и соответствовать критериям объективности. Данные требования нужно выполнять всегда, т.к. именно от них будет зависеть соответствие характеристик метода и характеристик того, что подвергается статистическому анализу.

Таким образом, перед обработкой выборочного материала необходимо провести его тщательную проверку, избавившись тем самым от всего ненужного и второстепенного. Одновременно с этим, составляя выборку, в обязательном порядке нужно обходить стороной любую самодеятельность. Это означает, что ни в коем случае не следует делать выборку только из вариантов, кажущихся типичными, а все другие – отбрасывать.

Эффективная и качественная выборка должна составляться объективно, т.е. производить ее нужно так, чтобы были исключены любые субъективные влияния и предвзятые побуждения. И чтобы это условие было соблюдено должным образом, требуется прибегнуть к принципу рандомизации или, проще говоря, к принципу случайного отбора вариантов из всей их генеральной совокупности.

Представленный принцип служит основой теории выборочного метода, и следовать ему нужно всегда, когда требуется создать эффективную выборочную совокупность, причем случаи планомерного отбора исключением здесь не являются.

Корреляционный анализ и регрессионный анализ – это два высокоэффективных метода, позволяющие проводить анализ больших объемов данных для изучения возможной взаимосвязи двух или большего количества показателей.

В случае с корреляционным анализом задачами являются:

• Измерить тесноту имеющейся связи дифференцирующихся признаков;
• Определить неизвестные причинные связи;
• Оценить факторы, в наибольшей степени воздействующие на окончательный признак.

А в случае с регрессионным анализом задачи следующие:

• Определить форму связи;
• Установить степень воздействия независимых показателей на зависимый;
• Определить расчетные значения зависимого показателя.

Чтобы решить все вышеназванные задачи, практически всегда нужно применять и корреляционный и регрессионный анализ в комплексе.

Посредством этого метода статистического анализа очень удобно определять интенсивность или скорость, с которой развиваются явления, находить тенденцию их развития, выделять колебания, сравнивать динамику развития, находить взаимосвязь развивающихся во времени явлений.

Ряд динамики – это такой ряд, в котором во времени последовательно расположены статистические показатели, изменения которых характеризуют процесс развития исследуемого объекта или явления.

Ряд динамики включает в себя два компонента:

• Период или момент времени, связанный с имеющимися данными;
• Уровень или статистический показатель.

В совокупности эти компоненты представляют собой два члена ряда динамики, где первый член (временной период) обозначается буквой «t», а второй (уровень) – буквой «y».

Исходя из длительности временных промежутков, с которыми взаимосвязаны уровни, ряды динамики могут быть моментными и интервальными. Интервальные ряды позволяют складывать уровни для получения общей величины периодов, следующих один за другим, а в моментных такой возможности нет, но этого там и не требуется.

Ряды динамики также существуют с равными и разными интервалами. Суть же интервалов в моментных и интервальных рядах всегда разная. В первом случае интервалом является временной промежуток между датами, к которым привязаны данные для анализа (удобно использовать такой ряд, например, для определения количества действий за месяц, год и т.д.). А во втором случае – временной промежуток, к которому привязана совокупность обобщенных данных (такой ряд можно использовать для определения качества тех же самых действий за месяц, год и т.п.). Интервалы могут быть равными и разными, независимо от типа ряда.

Естественно, чтобы научиться грамотно применять каждый из методов статистического анализа, недостаточно просто знать о них, ведь, по сути, статистика – это целая наука, требующая еще и определенных навыков и умений. Но чтобы она давалась проще, можно и нужно тренировать свое мышление и улучшать когнитивные способности.

В остальном же исследование, оценка, обработка и анализ информации – очень интересные процессы. И даже в тех случаях, когда это не приводит к какому-то конкретному результату, за время исследования можно узнать множество интересных вещей. Статистический анализ нашел свое применение в огромном количестве сфер деятельности человека, а вы можете использовать его в учебе, работе, бизнесе и других областях, включая развитие детей и самообразование.

источник

Во многих случаях связь между результативным и факторными показателями может моделироваться уравнением прямой линии (линейная связь).

Поведение результативного показателя может быть обусловлено влиянием одного (парная регрессия) или многих факторов (множественная регрессия).

Начнем рассмотрение с наиболее простых для анализа линейных связей, последовательно рассмотрев случаи парной и множественной регрессии.

Парная линейная регрессия характеризует связь между двумя признаками: результативным и факторным, и предполагается, что аналитически связь между ними описывается уравнением прямой линии: у-ал-Ьх.

Статистическое исследование начинается с проведения статистического наблюдения. Проводят случайную выборку. При значениях факторного показателя х_х, х₂, х₃. х_п мы наблюдаем значения результативного показателя y_t, у₂, у₃у. у_п соответственно (п — объем исследуемой совокупности, т.е. число единиц наблюдения). Па плоскости отмечаем точки с координатами (х„ у_х), (х₂, у₂), (х₃, уз). (x_w у_п).

Так как мы рассматриваем случай парной линейной регрессии, то предполагаем, что точки группируются вокруг некоторой прямой линии у-ал-Ьх.

Точки не находятся точно на линии у = ал-Ьх_у так как на поведение у

помимо фактора х оказывают влияние и другие факторы. Отклонение фактических значений результативного показателя от теоретических значений, полученных по выбранному уравнению регрессии, называется ошибкой (остатком, отклонением): г, -у_х -у_х.

Таким образом, фактическое значение результативного показателя

Отметим, что ошибка является случайной величиной.

Основные предпосылки модели парной линейной регрессии следующие [19]:

• • связь между переменными хну является линейной;
• • независимая переменная х может быть использована для прогноза у,
• • остатки (т.е. ошибки) нормально распределены;
• • для всех данных х математическое ожидание ошибки равно нулю и дисперсия ошибки постоянна;
• • ошибки независимы.

Оценка параметров уравнения регрессии а, b осуществляется методом наименьших квадратов. В основе метода наименьших квадратов лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного показателя от теоретических, полученных по выбранному уравнению регрессии:

где y_t — фактическое значение результативного показателя; у, — теоретическое значение результативного показателя, полученное по выбранному уравнению регрессии.

В случае парной линейной регрессии уравнение (9.1) принимает вид

Для нахождения параметров уравнения регрессии а, b необходимо найти производную и приравнять ее к нулю (задача на экстремум функции). В результате получим систему нормальных уравнений

Разрешив систему уравнений (9.2) относительно параметров а, Ь, получим

В уравнении регрессии параметр а показывает усредненное влияние на результативный показатель неучтенных в уравнении факторных признаков; коэффициент регрессии b показывает, на сколько единиц своего измерения изменяется в среднем значение результативного показателя при увеличении факторного на единицу собственного измерения. Знак коэффициент регрессии b позволяет сделать вывод о направлении связи. Положительное значение коэффициента регрессии b свидетельствует о том, что связь между результативным и факторным показателями прямая. Отрицательное значение коэффициента регрессии b свидетельствует о наличии между результативным и факторным показателями обратной связи.

Дальнейший анализ полученного уравнения регрессии у=а+Ьх позволяет ответить на вопрос, насколько сильно влияние неучтенных факторов, действительно ли модель линейна и т.д.

Пример 9.1. Имеются данные о динамике доходности акции конкретной корпорации (у) и динамике среднерыночной доходности (х) за восемь периодов:

На основании статистической информации построим уравнение линейной регрессии.

Результаты промежуточных вычислений представлены в табл. 9.3.

Результаты вычислений для примера 9.1

Итак, уравнение регрессии у =а + Ьх = 1,19 +1,125л:.

Связь между доходностью акции и среднерыночной доходностью прямая, о чем свидетельствует положительное значение коэффициента Ь, т.е. среднерыночная доходность и доходность акции изменяются однонаправленно. При увеличении среднерыночной доходности па 1% доходность акции в среднем увеличится на 1,125%.

Часто результативный показатель зависит не от одного, а от многих факторов. Тогда вместо парной регрессии используют множественную регрессию. Построение моделей множественной регрессии должно включать следующие этапы:

• • выбор формы связи (уравнения регрессии);
• • отбор факторных признаков;
• • обеспечение достаточного объема совокупности.

Выбор типа уравнения затрудняется тем, что для любой формы зависимости можно выбрать целый ряд уравнений, которые в определенной степени будут описывать эти связи. Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации.

Важным этапом построения уже выбранного уравнения множественной регрессии являются отбор и последующее включение факторных признаков. Как уже отмечалось выше, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема. Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам.

Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена на основе интуитивно-логических или многомерных статистических методов анализа. Одним из способов отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ).

Метод шаговой регрессии предполагает последовательное включение факторов в уравнение регрессии и последующую проверку их значимости. Факторы поочередно вводятся в уравнение. При проверке значимости введенного фактора определяется, на сколько уменьшается сумма квадратов отклонений и увеличивается величина множественного коэффициента корреляции (методика расчета коэффициентов корреляции будет рассмотрена в параграфе 9.3). Одновременно используется и обратный метод, т.е. исключение факторов, ставших незначимыми.

Фактор является незначимым, если его включение в уравнение регрессии только изменяет значения коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициента регрессии — не изменяется (или меняется несущественно), то данный признак существенен и его включение в уравнение регрессии необходимо. В противном случае фактор нецелесообразно включать в модель регрессии [1] .

При построении модели регрессии возможна проблема мультиколлинеарности.

Мультиколлинеарность — это линейная взаимосвязь двух или нескольких факторных признаков, включенных в модель.

Наличие мультиколлинеарности между признаками приводит к следующим последствиям:

• • искажению величины параметров модели, которые имеют тенденцию к завышению, чем осложняется процесс определения наиболее существенных факторных признаков;
• • изменению смысла экономической интерпретации коэффициентов регрессии.

В качестве причин возникновения мультиколлинеарности между признаками можно выделить следующие:

• • изучаемые факторные признаки являются характеристикой одной и той же стороны явления или процесса;
• • факторные признаки являются составляющими элементами друг друга;
• • факторные признаки по экономическому смыслу дублируют друг друга.

Отметим, что не всегда имеет смысл прилагать существенные усилия по выявлению и устранению мультиколлинеарности. Все зависит от цели исследования. Если основная цель модели — прогноз будущих значений результативного признака, то при значениях коэффициента детерминации (методика его определения будет рассмотрена в параграфе 9.3) г 2 >0,9 наличие мультиколлинеарности обычно не сказывается на прогнозных качествах модели.

Существуют различные методы устранения мультиколлинеарпости. Простейшим методом является исключение из модели одного или нескольких линейно-связанных факторных признаков. Вопрос о том, какой из факторов следует отбросить, решается на основании качественного и логического анализа изучаемого явления.

В прикладных моделях лучше не сокращать число факторов до тех пор, пока мультиколлинеарность не станет серьезной проблемой.

Иногда проблема мультиколлинеарности может быть решена путем изменения спецификации модели.

Множественная линейная регрессия характеризует связь между результативным и несколькими факторными признаками, и предполагается наличие линейной связи между ними:

где т — число объясняющих переменных (факторов); а, а_х, а₂,а_т — параметры модели.

Для обеспечения статистической надежности требуется выполнение условия п > 3(/72 4-1), где п — число наблюдений.

Основные предпосылки модели множественной линейной регрессии следующие 1191:

• • математическое ожидание случайного отклонения е, равно нулю для всех наблюдений;
• • дисперсии отклонений постоянны и равны для всех наблюдений;
• • случайные отклонения независимы друг от друга;
• • случайное отклонение независимо от объясняющих переменных (факторных показателей);
• • модель линейна относительно параметров;
• • между факторами отсутствует строгая линейная связь;
• • случайные отклонения г, распределены нормально с параметрами 0 и а 2 . Параметры уравнения множественной линейной регрессии могут быть

определены методом наименьших квадратов. Методика построения уравнения множественной линейной регрессии аналогична случаю парной линейной регрессии. Вместо переменных подставляются результаты наблюдений, находятся остатки и минимизируется сумма квадратов остатков.

Рассмотрим построение уравнения регрессии при наличии связи между результативным и двумя факторными признаками (т = 2):

В соответствии с методом наименьших квадратов сумма квадратов отклонений фактического значения результативного показателя от теоретического должна быть минимальна (см. формулу (9.1)).

В случае множественной линейной регрессии при наличии связи между результативным и двумя факторными признаками задача (9.1) принимает вид

Минимизируя сумму квадратов отклонений, получаем систему нормальных уравнений

Разрешив систему уравнений (9.4) относительно параметров а, a_t, а₂, получим

Пример 9.2. Объем продаж у линейно зависит от цены товара х, и затрат на рекламу х₂. Статистические данные собраны за 7 мес.:

источник

Для удобства изучения материала статью Регрессионный анализ разбиваем на темы:

Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.

Корреляционный анализ и регрессионный анализ являются смежными разделами математической статистики, и предназначаются для изучения по выборочным данным статистической зависимости ряда величин; некоторые из которых являются случайными. При статистической зависимости величины не связаны функционально, но как случайные величины заданы совместным распределением вероятностей.

Исследование зависимости случайных величин приводит к моделям регрессии и регрессионному анализу на базе выборочных данных. Теория вероятностей и математическая статистика представляют лишь инструмент для изучения статистической зависимости, но не ставят своей целью установление причинной связи. Представления и гипотезы о причинной связи должны быть привнесены из некоторой другой теории, которая позволяет содержательно объяснить изучаемое явление.

Числовые данные обычно имеют между собой явные (известные) или неявные (скрытые) связи.

Явно связаны показатели, которые получены методами прямого счета, т. е. вычислены по заранее известным формулам. Например, проценты выполнения плана, уровни, удельные веса, отклонения в сумме, отклонения в процентах, темпы роста, темпы прироста, индексы и т. д.

Связи же второго типа (неявные) заранее неизвестны. Однако необходимо уметь объяснять и предсказывать (прогнозировать) сложные явления для того, чтобы управлять ими. Поэтому специалисты с помощью наблюдений стремятся выявить скрытые зависимости и выразить их в виде формул, т. е. математически смоделировать явления или процессы. Одну из таких возможностей предоставляет корреляционно-регрессионный анализ.

Математические модели строятся и используются для трех обобщенных целей:

* для объяснения;
* для предсказания;
* для управления.

Пользуясь методами корреляционно-регрессионного анализа, аналитики измеряют тесноту связей показателей с помощью коэффициента корреляции. При этом обнаруживаются связи, различные по силе (сильные, слабые, умеренные и др.) и различные по направлению (прямые, обратные). Если связи окажутся существенными, то целесообразно будет найти их математическое выражение в виде регрессионной модели и оценить статистическую значимость модели.

Регрессионный анализ называют основным методом современной математической статистики для выявления неявных и завуалированных связей между данными наблюдений.

Постановка задачи регрессионного анализа формулируется следующим образом.

Имеется совокупность результатов наблюдений. В этой совокупности один столбец соответствует показателю, для которого необходимо установить функциональную зависимость с параметрами объекта и среды, представленными остальными столбцами. Требуется: установить количественную взаимосвязь между показателем и факторами. В таком случае задача регрессионного анализа понимается как задача выявления такой функциональной зависимости y = f (x2, x3, …, xт), которая наилучшим образом описывает имеющиеся экспериментальные данные.

— количество наблюдений достаточно для проявления статистических закономерностей относительно факторов и их взаимосвязей;
— обрабатываемые данные содержат некоторые ошибки (помехи), обусловленные погрешностями измерений, воздействием неучтенных случайных факторов;
— матрица результатов наблюдений является единственной информацией об изучаемом объекте, имеющейся в распоряжении перед началом исследования.

Функция f (x2, x3, …, xт), описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии. Термин «регрессия» (regression (лат.) – отступление, возврат к чему-либо) связан со спецификой одной из конкретных задач, решенных на стадии становления метода.

Решение задачи регрессионного анализа целесообразно разбить на несколько этапов:

— предварительная обработка данных;
— выбор вида уравнений регрессии;
— вычисление коэффициентов уравнения регрессии;
— проверка адекватности построенной функции результатам наблюдений.

Предварительная обработка включает стандартизацию матрицы данных, расчет коэффициентов корреляции, проверку их значимости и исключение из рассмотрения незначимых параметров.

Выбор вида уравнения регрессии Задача определения функциональной зависимости, наилучшим образом описывающей данные, связана с преодолением ряда принципиальных трудностей.

В общем случае для стандартизованных данных функциональную зависимость показателя от параметров можно представить в виде:

где f — заранее не известная функция, подлежащая определению;
e — ошибка аппроксимации данных.

Указанное уравнение принято называть выборочным уравнением регрессии. Это уравнение характеризует зависимость между вариацией показателя и вариациями факторов. А мера корреляции измеряет долю вариации показателя, которая связана с вариацией факторов. Иначе говоря, корреляцию показателя и факторов нельзя трактовать как связь их уровней, а регрессионный анализ не объясняет роли факторов в создании показателя.

Еще одна особенность касается оценки степени влияния каждого фактора на показатель. Регрессионное уравнение не обеспечивает оценку раздельного влияния каждого фактора на показатель, такая оценка возможна лишь в случае, когда все другие факторы не связаны с изучаемым. Если изучаемый фактор связан с другими, влияющими на показатель, то будет получена смешанная характеристика влияния фактора. Эта характеристика содержит как непосредственное влияние фактора, так и опосредованное влияние, оказанное через связь с другими факторами и их влиянием на показатель.

В регрессионное уравнение не рекомендуется включать факторы, слабо связанные с показателем, но тесно связанные с другими факторами. Не включают в уравнение и факторы, функционально связанные друг с другом (для них коэффициент корреляции равен 1). Включение таких факторов приводит к вырождению системы уравнений для оценок коэффициентов регрессии и к неопределенности решения.

Функция f должна подбираться так, чтобы ошибка e в некотором смысле была минимальна. В целях выбора функциональной связи заранее выдвигают гипотезу о том, к какому классу может принадлежать функция f, а затем подбирают «лучшую» функцию в этом классе. Выбранный класс функций должен обладать некоторой «гладкостью», т.е. «небольшие» изменения значений аргументов должны вызывать «небольшие» изменения значений функции.

Частным случаем, широко применяемым на практике, является полином первой степени или уравнение линейной регрессии.

Для выбора вида функциональной зависимости можно рекомендовать следующий подход:

— в пространстве параметров графически отображают точки со значениями показателя. При большом количестве параметров можно строить точки применительно к каждому из них, получая двумерные распределения значений;
— по расположению точек и на основе анализа сущности взаимосвязи показателя и параметров объекта делают заключение о примерном виде регрессии или ее возможных вариантах;
— после расчета параметров оценивают качество аппроксимации, т.е. оценивают степень близости расчетных и фактических значений;
— если расчетные и фактические значения близки во всей области задания, то задачу регрессионного анализа можно считать решенной. В противном случае можно попытаться выбрать другой вид полинома или другую аналитическую функцию, например периодическую.

Вычисление коэффициентов уравнения регрессии

Систему уравнений на основе имеющихся данных однозначно решить невозможно, так как количество неизвестных всегда больше количества уравнений. Для преодоления этой проблемы нужны дополнительные допущения. Здравый смысл подсказывает: желательно выбрать коэффициенты полинома так, чтобы обеспечить минимум ошибки аппроксимации данных. Могут применяться различные меры для оценки ошибок аппроксимации. В качестве такой меры нашла широкое применение среднеквадратическая ошибка. На ее основе разработан специальный метод оценки коэффициентов уравнений регрессии – метод наименьших квадратов (МНК). Этот метод позволяет получить оценки максимального правдоподобия неизвестных коэффициентов уравнения регрессии при нормальном распределения вариант, но его можно применять и при любом другом распределении факторов.

В основе МНК лежат следующие положения:

— значения величин ошибок и факторов независимы, а значит, и некоррелированы, т.е. предполагается, что механизмы порождения помехи не связаны с механизмом формирования значений факторов;
— математическое ожидание ошибки e должно быть равно нулю (постоянная составляющая входит в коэффициент a0), иначе говоря, ошибка является центрированной величиной;
— выборочная оценка дисперсии ошибки должна быть минимальна.

Если же линейная модель неточна или параметры измеряются неточно, то и в этом случае МНК позволяет найти такие значения коэффициентов, при которых линейная модель наилучшим образом описывает реальный объект в смысле выбранного критерия среднеквадратического отклонения.

Качество полученного уравнения регрессии оценивают по степени близости между результатами наблюдений за показателем и предсказанными по уравнению регрессии значениями в заданных точках пространства параметров. Если результаты близки, то задачу регрессионного анализа можно считать решенной. В противном случае следует изменить уравнение регрессии и повторить расчеты по оценке параметров.

При наличии нескольких показателей задача регрессионного анализа решается независимо для каждого из них.

Анализируя сущность уравнения регрессии, следует отметить следующие положения. Рассмотренный подход не обеспечивает раздельной (независимой) оценки коэффициентов — изменение значения одного коэффициента влечет изменение значений других. Полученные коэффициенты не следует рассматривать как вклад соответствующего параметра в значение показателя. Уравнение регрессии является всего лишь хорошим аналитическим описанием имеющихся данных, а не законом, описывающим взаимосвязи параметров и показателя. Это уравнение применяют для расчета значений показателя в заданном диапазоне изменения параметров. Оно ограниченно пригодно для расчета вне этого диапазона, т.е. его можно применять для решения задач интерполяции и в ограниченной степени для экстраполяции.

Главной причиной неточности прогноза является не столько неопределенность экстраполяции линии регрессии, сколько значительная вариация показателя за счет неучтенных в модели факторов. Ограничением возможности прогнозирования служит условие стабильности неучтенных в модели параметров и характера влияния учтенных факторов модели. Если резко меняется внешняя среда, то составленное уравнение регрессии потеряет свой смысл.

Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения параметра, является точечным. Вероятность реализации такого прогноза ничтожна мала. Целесообразно определить доверительный интервал прогноза. Для индивидуальных значений показателя интервал должен учитывать ошибки в положении линии регрессии и отклонения индивидуальных значений от этой линии.

Для проведения регрессионного анализа необходимо следующее:

• Выбор одного блока, из которого берется координатный интервал, чьи данные (переменная значения) дают зависимую переменную регрессии. Например, в качестве переменной Y из блока заболеваемости берется обращаемость в координатном интервале «пневмония» координаты «диагноз».

• Выбор одного или нескольких блоков, из которых аналогично берутся факторы в качестве независимых переменных регрессии. Например, данные в координатном интервале «концентрация SO2» берутся в качестве X1, а в координатном интервале «скорость ветра» — в качестве X2. При этом необходимо, чтобы блок, дающий зависимую переменную, и все блоки, дающие независимые переменные, имели какие-либо общие координаты (обычно пространство и время), которые служат переменными развертки и дают точки, по которым проводится регрессионная кривая или поверхность.

• Выбор типа и «степени» функций от независимых переменных, которые включаются в регрессию. Например, при выборе полиномиальных функций с максимальной степенью 2 и при двух независимых переменных X1 и X2 регрессия ищется в виде

Y = a + bX1 + cX2 + dX12 + eX22 + fX1X2
(a — f -регрессионные коэффициенты).

• Задание координатных интервалов переменных сравнения, внутри которых регрессионная функция не должна значимо изменяться. Так, в вышеописанном случае можно потребовать, чтобы регрессионная функция вообще не зависела от половозрастной группы, или была одной для всех мужчин и другой — для всех женщин, или своей в каждой половозрастной группе. Эта информация используется для регуляризации регрессии гребневым или энтропийным методом.

• Регрессия проводится последовательно с увеличением числа независимых переменных и степени регрессионной функции. При этом общесистемным оптимизатором находится минимум среднеквадратичного отклонения точек данных от регрессионной кривой.

Для регрессионной кривой вычисляются характеристики неопределенности — показатели тесноты регрессии: кривые доверительного интервала и коэффициент детерминации. Последний может вычисляться сразу для всех комбинаций «зависимая переменная — независимая переменная» и представляться в виде цветокодированной таблицы. Такое представление близко к цветокодированию коэффициента корреляции. Разница между ними связана с возможностью выбора типа и степени регрессионной функции при регрессионном анализе.

Аналогично построению таблицы условных корреляций, в регрессионном анализе может строиться таблица «условных» коэффициентов детерминации. При этом в регрессию для каждой пары факторов дополнительно включается еще несколько факторов, выбранных пользователем. Например, строятся регрессии данных обращаемости по каждому диагнозу на концентрацию каждого загрязнителя, и при этом в регрессию дополнительно включается в качестве независимой переменной скорость ветра. Сравнение таких таблиц с аналогичными «безусловными» позволяет определить, в какие регрессии нужно дополнительно включить факторы, выбранные пользователем в качестве условных.

Как и для коэффициентов корреляции, для коэффициентов детерминации можно строить дерево вкладов координатных интервалов переменных развертки. Оно позволяет скорректировать выборку для достижения более тесной регрессии. Кроме того, выбрав координатный интервал в дереве, можно построить отдельные регрессионные функции во всех его подынтервалах и по результатам расслоить выборку на части с более устойчивой регрессией. В частности, можно построить «иерархическую регрессию», при которой коэффициенты регрессии внутри каждого координатного интервала рассчитываются как поправки к коэффициентам регрессии координатного интервала, следующего вверх по иерархии. При использовании такой регрессии в качестве эмпирической модели, разные коэффициенты выступают как варианты модели.

Как и корреляция, регрессия рассчитывается для фиксированных координатных интервалов каждой переменной сравнения. Как указано выше, проверяется устойчивость регрессии к смене координатного интервала на том же уровне иерархии. Строится также дерево вкладов подынтервалов для выбранных пользователем переменной сравнения и координатного интервала. Возможно также построение иерархической регрессии по дереву выбранной переменной сравнения. При этом, в отличие от иерархической регрессии по дереву переменной значения, разные регрессии в дереве выступают не как варианты, а применяются соответственно значениям переменных сравнения, подаваемым на вход модели. Возможно также построение отдельной регрессии для каждого диапазона значений независимой или зависимой переменной. В первом случае получаются сплайны с числом узлов, задаваемым пользователем. Во втором случае различные регрессии образуют пакет вариантов, так что выбор подходящего диапазона при использовании такой регрессии в качестве эмпирической модели осуществляется в рамках общей идеологии выбора оптимального варианта.

Для визуализации многофакторной регрессии пользователь выбирает тот фактор, который представляется как абсцисса регрессионной кривой, и фиксирует значения прочих независимых факторов. На коэффициенты регрессии это не влияет.

Термин «регрессия» ввел английский психолог и антрополог Ф.Гальтон.

Для точного описания уравнения регрессии необходимо знать чакон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии ffc), так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результатирующего показателя у при заданных значениях аргумента х.

Рассмотрим взаимоотношение между истинной f (х) = = М(у/х), модельной регрессией у и оценкой у регрессии.

Пусть результативный показатель у связан с аргументом х соотношением:

у=2х 1,5+o
где o – случайная величина, имеющая нормальный закон распределения.
Причем M o= 0 и d o– o 2.

Истинная функция регрессии в этом случае имеет вид:

Для наилучшего восстановления по исходным статистическим данным условного значения результативного показателя f(x) и неизвестной функции регрессии /(х) = М(у/х) наиболее часто используют следующие критерии адекватности (функции потерь). Согласно методу наименьших квадратов минимизируется квадрат отклонения наблюдаемых значений результативного показателя y(i = 1, 2, . п)от модельных значений y i= f(х i),где х i– значение вектора аргументов в i-м наблюдении:

Получаемая регрессия называется среднеквадратической.

Согласно методу наименьших модулей, минимизируется сумма абсолютных отклонений наблюдаемых значений результативного показателя от модульных значений:

И получаем среднеабсолютную медианную регрессию:

Регрессионный анализ – это метод статистического анализа зависимости случайной величины уот переменных х j(j=1,2, . k), рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения х j.

Анализ данных — область информатики, занимающаяся построением и исследованием наиболее общих математических методов и вычислительных алгоритмов извлечения знаний из экспериментальных (в широком смысле) данных.

Ms Excel представляет широкие возможности для проведения анализа данных, находящихся в списке.

К средствам анализа относятся:

• Обработка списка с помощью различных формул и функций;
• Построение диаграмм и использование карт Ms Excel;
• Проверка данных рабочих листов и рабочих книг на наличие ошибок;
• Структуризация рабочих листов;
• Автоматическое подведение итогов (включая мастер частичных сумм);
• Консолидация данных;
• Сводные таблицы;
• Специальные средства анализа выборочных записей и данных — подбор параметра, поиск решения, сценарии и др.

В состав Microsoft Excel входит набор средств анализа данных (так называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие средства позволяют представить результаты анализа в графическом виде.

Статистические данные приводятся в виде длинных и сложных статистических таблиц, поэтому бывает весьма трудно обнаружить в них имеющиеся неточности и ошибки.

Графическое же представление статистических данных помогает легко и быстро выявить ничем не оправданные пики и впадины, явно не соответствующие изображаемым статистическим данным, аномалии и отклонения.

Графическое представление статистических данных является не только средством иллюстрации статистических данных и контроля их правильности и достоверности. Благодаря своим свойствам оно является важным средством толкования и анализа статистических данных, а в некоторых случаях — единственным и незаменимым способом их обобщения и познания.

Регрессия является инструментом пакета анализа данных Microsoft Excel. Линейный регрессионный анализ заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных.

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными и одной зависимой переменной. В нашем случае, это анализ связи между значениями индикаторов и движением цены.

В самом простом виде такое уравнение может иметь вид:

Изменение цены = a * RSI + b * MACD + с

Построить регрессионное уравнение можно только при наличии корреляции между независимыми переменными и зависимой. Поскольку значения индикаторов, как правило, имеют связь друг с другом, то вклад индикаторов в предсказание может существенно меняться, если мы добавим или уберем какой-либо индикатор из анализа. Обратите внимание, что регрессионное уравнение – это только демонстрация числовой зависимости, а не описание причинных связей. Коэффициенты (a, b) показывают вклад каждой независимой переменной в связь с зависимой.

Регрессионное уравнение выражает идеальную зависимость переменных. Однако, на форекс такое невозможно, поэтому прогноз всегда будет отличаться от реальности. Разница между прогнозируемым значением и реальным называется остатком. Анализ остатков позволяет определить, в том числе, наличие нелинейной зависимости между индикатором и ценой. В нашем случае мы предполагаем, что между индикаторами и ценой есть только линейная зависимость. К счастью, регрессионный анализ устойчив к малым отклонениям от линейности.

Регрессионный анализ может быть использован только для анализа количественных показателей. Качественные показатели, которые не имеют переходных значений, не подходят для этого анализа.

Поскольку регрессионный анализ может «перемолоть» любое число показателей, то возникает соблазн включить в него их как можно больше. Однако если число независимых показателей будет больше, чем число наблюдений их взаимодействия с зависимым показателем, тогда есть большая вероятность получить уравнения с хорошими предсказаниями, но основанными на случайных колебаниях.

Число наблюдений должно быть в 10-20 раз больше, чем число независимых показателей.

В нашем случае количество индикаторов, которое содержит наша выборка данных, должно быть в 10-20 раз больше, чем число сделок в нашей выборке. Тогда полученное уравнение будет считаться надежным. В выборке, на основе которой был сделан робот в разделе 1, содержалось 33 показателя и 836 наблюдений. В результате число показателей было в 25 раз больше, чем число наблюдений. Это требование является общим правилом для статистики. Оно же действует и для оптимизатора тестера стратегий терминала MetaTrader 5.

При этом в оптимизаторе каждое заданное значение индикатора фактически является отдельным показателем. Другими словами, если мы тестируем 10 значений для индикатора, то это 10 независимых показателей, это следует учитывать, чтобы избежать переоптимизации. Возможно, в отчет оптимизатора следует добавить показатель: среднее количество сделок/количество значений всех оптимизируемых параметров. Если значение показателя будет меньше десяти, то высока вероятность переоптимизации.

Другое, что нужно учитывать, это выбросы в данных. Редкие, но сильные события (в нашем случае скачки цены) могут внести ложные зависимости в уравнение. Например, после выхода какой-либо неожиданной новости на рынке произошло сильное движение, продлившееся несколько часов. В этом случае значения технических индикаторов имели малую значимость в прогнозе, но регрессионный анализ припишет им высокую значимость, поскольку было сильное изменение цены. Поэтому желательно фильтровать данные в выборке или проверять наличие выбросов в данных.

Следующий пример использует файл данных Poverty. sta. Открыть его можно с помощью меню Файл, выбрав команду Открыть; наиболее вероятно, что этот файл данных находится в директории /Examples/Datasets. Данные основаны на сравнении результатов переписи 1960 и 1970 годов для случайной выборки из 30 округов. Имена округов введены в качестве идентификаторов наблюдений.

Следующая информация по каждой переменной приводится в электронной таблице Редактор спецификаций переменных (открывающийся при выборе команды Все спецификации переменных. в меню Данные).

Цель исследования. Мы проанализируем корреляты бедности (т.е. предикторы, «сильно» коррелирующие с процентом семей, живущих за чертой бедности). Таким образом, будем рассматривать переменную 3 (Pt_Poor), как зависимую или критериальную переменную, а все остальные переменные — в качестве независимых переменных или предикторов.

Начальный анализ. Когда вы выбираете команду Множественной регрессии с помощью меню Анализ, открывается стартовая панель модуля Множественная регрессия. Вы можете задать регрессионное уравнение щелчком мыши по кнопке Переменные во вкладке Быстрый стартовой панели модуля Множественная регрессия. В появившемся окне Выбора переменных выберите Pt_Poor в качестве зависимой переменной, а все остальные переменные набора данных — в качестве независимых. Во вкладке Дополнительно отметьте также опции Показывать описательные статистики, корр. матрицы.

Теперь нажмите OK этого диалогового окна, после чего откроется диалоговое окно Просмотр описательных статистик. Здесь вы можете просмотреть средние и стандартные отклонения, корреляции и ковариации между переменными. Отметим, что это диалоговое окно доступно практически из всех последующих окон модуля Множественная регрессия, так что вы всегда сможете вернуться назад, чтобы посмотреть на описательные статистики определенных переменных.

Распределение переменных. Сначала изучим распределение зависимой переменной Pt_Poor по округам. Нажмите Средние и стд.отклонения для показа таблицы результатов.

Выберите Гистограммы в меню Графика, чтобы построить гистограмму для переменной Pt_Poor (во вкладке Дополнительно диалогового окна 2М Гистограммы установите опцию Число категорий в строке Категории равной 16). Как видно ниже, распределение этой переменной чем-то отличается от нормального распределения. Коэффициенты корреляции могут оказаться существенно завышенными или заниженными при наличии в выборке существенных выбросов. Однако, хотя два округа (две самые правые колонки) имеют более высокий процент семей, проживающих за чертой бедности, чем это можно было бы ожидать в соответствии с нормальным распределением, они все еще, как нам кажется, находятся «в рамках допустимого».

Это решение является в определенной степени субъективным; эмпирическое правило состоит в том, что беспокойство требуется проявлять только тогда, когда наблюдение (или наблюдения) лежат вне интервала, заданного средним значением ± 3 стандартных отклонения. В этом случае будет разумно повторить критическую (с точки зрения влияния выбросов) часть анализа с выбросами и без них, с тем, чтобы удостовериться в отсутствии их влияния на характер взаимных корреляций. Вы также можете просмотреть распределение этой переменной, щелкнув мышкой по кнопке Диаграмма размаха во вкладке Дополнительно диалогового окна Просмотр описательных статистик, выбрав переменную Pt_Poor. Далее, выберите опцию Медиана/квартили/размах в диалоговом окне Диаграммы размаха и нажмите кнопку OK.

(Заметим, что определенный метод вычисления медианы и квартилей может быть выбран для всей «системы» в диалоговом окне Параметры в меню Сервис.)

Диаграммы рассеяния. Если имеются априорные гипотезы о связи между определенными переменными, на этом этапе может оказаться полезным вывести соответствующую диаграмму рассеяния. Например, посмотрим на связь между изменением популяции и процентом семей, проживающих за чертой бедности. Было бы естественно ожидать, что бедность приводит к миграции населения; таким образом, должна наблюдаться отрицательная корреляция между процентом семей, проживающих за чертой бедности, и изменением популяции.

Возвратимся к диалоговому окну Просмотр описательных статистик и щелкнем мышкой по кнопке Корреляции во вкладке Быстрый для отображения таблицы результатов с корреляционной матрицей.

Корреляции между переменными могут быть отображены также и на матричной диаграмме рассеяния. Матричная диаграмма рассеяния для выбранных переменных может быть получена щелчком мыши по кнопке Матричный график корреляций во вкладке Дополнительно диалогового окна Просмотр описательных статистик и последующим выбором интересующих переменных.

Задание множественной регрессии. Для выполнения регрессионного анализа от вас требуется только щелкнуть по кнопке OK в диалоговом окне Просмотр описательных статистик и перейти в окно Результаты множественной регрессии. Стандартный регрессионный анализ (со свободным членом) будет выполнен автоматически.

Просмотр результатов. Ниже изображено диалоговое окно Результаты множественной регрессии. Общее уравнение множественной регрессии высоко значимо (см. главу Элементарные понятия статистики по поводу обсуждения проверки статистической значимости). Таким образом, зная значения независимых переменных, можно «предсказать» предиктор, связанный с бедностью, лучше, чем угадывая его чисто случайно.

Регрессионные коэффициенты. Чтобы узнать, какие из независимых переменных дают больший вклад в предсказание предиктора, связанного с бедностью, изучим регрессионные (или B) коэффициенты. Щелкните мышкой по кнопке Итоговая таблица регрессии во вкладке Быстрый диалогового окна Результаты множественной регрессии для вывода таблицы результатов с этими коэффициентами.

Эта таблица показывает стандартизованные регрессионные коэффициенты (Бета) и обычные регрессионные коэффициенты (B). Бета-коэффициенты — это коэффициенты, которые получатся, если предварительно стандартизовать все переменные к среднему 0 и стандартному отклонению 1. Таким образом, величина этих Бета-коэффициентов позволяет сравнивать относительный вклад каждой независимой переменной в предсказание зависимой переменной. Как видно из таблицы результатов, изображенной выше, переменные Pop_Chng, Pt_Rural и N_Empld являются наиболее важными предикторами для бедности; из них только первые два статистически значимы. Регрессионный коэффициент для Pop_Chng отрицателен; т.е. чем меньше прирост популяция, тем большее число семей живут ниже уровня бедности в соответствующем округе. Вклад в регрессию для Pt_Rural положителен; т.е. чем больше процент сельского населения, тем выше уровень бедности.

Частные корреляции. Другой путь изучения вкладов каждой независимой переменной в предсказание зависимой переменной состоит в вычислении частных и получастных корреляций (щелкните на кнопке Частные корреляции во вкладке Дополнительно диалогового окна Результаты множественной регрессии). Частные корреляции являются корреляциями между соответствующей независимой переменной и зависимой переменной, скорректированными относительно других переменных. Таким образом, это корреляция между остатками после корректировки относительно независимых переменных. Частная корреляция представляет самостоятельный вклад соответствующей независимой переменной в предсказание зависимой переменной.

Получастные корреляция являются корреляциями между соответствующей независимой переменной, скорректированной относительно других переменных, и исходной (нескорректированной) зависимой переменной. Таким образом, получастная корреляция является корреляцией соответствующей независимой переменной после корректировки относительно других переменных, и нескорректированными исходными значениями зависимой переменной. Иначе говоря, квадрат получастной корреляции является показателем процента Общей дисперсии, самостоятельно объясняемой соответствующей независимой переменной, в то время как квадрат частной корреляции является показателем процента остаточной дисперсии, учитываемой после корректировки зависимой переменной относительно независимых переменных.

В этом примере частные и получастные корреляции имеют близкие значения. Однако иногда их величины могут различаться значительно (получастная корреляция всегда меньше). Если получастная корреляция очень мала, в то время как частная корреляция относительно велика, то соответствующая переменная может иметь самостоятельную «часть» в объяснении изменчивости зависимой переменной (т.е. «часть», которая не объясняется другими переменными). Однако в смысле практической значимости, эта часть может быть мала, и представлять только небольшую долю от общей изменчивости.

Анализ остатков. После подбора уравнения регрессии всегда полезно изучить полученные предсказанные значения и остатки. Например, экстремальные выбросы могут существенно сместить результаты и привести к ошибочным заключениям. Во вкладке Остатки/предложения/наблюдаемые нажмите кнопку Анализ остатков для перехода в соответствующее диалоговое окно.

Построчный график остатков. Эта опция диалогового окна предоставляет вам возможность выбрать один из возможных типов остатков для построения построчного графика. Обычно, следует изучить характер исходных (нестандартизованных) или стандартизованных остатков для идентификации экстремальных наблюдений. В нашем примере, выберите вкладку Остатки и нажмите кнопку Построчные графики остатков; по умолчанию будет построен график исходных остатков; однако, вы можете изменить тип остатков в соответствующем поле.

Масштаб, используемый в построчном графике в самой левой колонке, задается в терминах сигмы, т.е. стандартного отклонения остатков. Если один или несколько наблюдений попадают за границы ± 3 * сигма, то, вероятно, следует исключить соответствующие наблюдения (это легко достигается с помощью условий отбора) и выполнить анализ снова, чтобы убедиться в отсутствии смещения ключевых результатов, вызванного этими выбросами в данных.

Построчный график выбросов. Быстрый способ идентификации выбросов состоит в использовании опции График выбросов во вкладке Выбросы. Вы можете выбрать просмотр всех стандартных остатков, выпадающих за границы ± 2-5 сигма, или просмотр 100 наиболее выделяющихся наблюдений, выбранных в поле Тип выброса во вкладке Выбросы. При использовании опции Стандартный остаток (>2*сигма) в нашем примере какие-либо выбросы не заметны.

Расстояния Махаланобиса. Большинство учебников по статистике отводят определенное место для обсуждения темы выбросов и остатков для зависимой переменной. Однако роль выбросов для набора независимых переменных часто упускается из виду. Со стороны независимых переменных, имеется список переменных, участвующий с различными весами (регрессионные коэффициенты) в предсказании зависимой переменной. Независимые переменные можно представить себе в виде точек некоторого многомерного пространства, в котором может располагаться каждое наблюдение. Например, если вы имеете две независимые переменные с равными регрессионными коэффициентами, то можно построить диаграмму рассеяния этих двух переменных и расположить каждое наблюдение на этом графике. Вы можете затем нарисовать точку средних значений обоих переменных и вычислить расстояния от каждого наблюдения до этого среднего (называемого теперь центроидом) в этом двумерном пространстве; в этом состоит концептуальная идея, стоящая за вычислением расстояний Махаланобиса. Теперь посмотрим на эти расстояния, отсортированные по величине, с целью идентификации экстремальных наблюдений по независимым переменным. В поле Тип выбросов отметьте опцию расстояний Махаланобиса и нажмите кнопку Построчный график выбросов. Полученный график показывает расстояния Махаланобиса, отсортированные в порядке убывания.

Отметим, что округ Shelby оказывается в чем-то выделяющимся по сравнению с другими округами на графике. Если посмотреть на исходные данные, можно обнаружить, что в действительности округ Shelby — значительно больший по размеру округ с большим числом людей, занятых сельским хозяйством (переменная N_Empld), и намного более весомой популяцией афроамериканцев. Вероятно, было бы разумно выражать эти числа в процентах, а не в абсолютных значениях, в этом случае расстояние Махаланобиса округа Shelby от других округов в данном примере не было бы столь велико. Однако мы получили, что округ Shelby оказывается явным выбросом.

Удаленные остатки. Другой очень важной статистикой, позволяющей оценить масштаб проблемы выбросов, являются удаленные остатки. Они определяются как стандартизованные остатки для соответствующих наблюдений, которые получились бы при исключении соответствующих наблюдений из анализа. Напомним, что процедура множественной регрессии подбирает прямую линию для выражения взаимосвязи между зависимой и независимыми переменными. Если одно из наблюдений является очевидным выбросом (как округ Shelby в этих данных), то линия регрессии стремиться «приблизится» к этому выбросу, с тем чтобы учесть его, насколько это возможно. В результате, при исключении соответствующего наблюдения, возникнет совершенно другая линия регрессии (и B-коэффициенты). Поэтому, если удаленный остаток сильно отличается от стандартизованного остатка, у вас есть основания полагать, что результаты регрессионного анализа существенно смещены соответствующим наблюдением. В данном примере удаленный остаток для округа Shelby является выбросом, который существенно влияет на анализ. Вы можете построить диаграмму рассеяния остатков относительно удаленных остатков с помощью опции Остатки и удалить остатки во вкладке Диаграммы рассеяния. Ниже на диаграмме рассеяния явно заметен выброс.

STATISTICA предоставляет интерактивное средство для удаления выбросов (Кисть на панели инструментов для графики;). Позволяющее экспериментировать с удалением выбросов и позволяющее сразу же увидеть их влияние на линию регрессии. Когда это средство активизировано, курсор меняется на крестик и рядом с графиком высвечивается диалоговое окно Закрашивание. Вы можете (временно) интерактивно исключать отдельные точки данных из графика, отметив (1) опцию Автообновление и (2) поле Выключить из блока Операция; а затем щелкнув мышкой на точке, которую нужно удалить, совместив ее с крестиком курсора.

Отметим, что удаленные точки можно «возвратить», щелкнув по кнопке Отменить все в диалоговом окне Закрашивание.

Нормальные вероятностные графики. Из окна Анализ остатков пользователь получает большому количеству дополнительных графиков. Большинство этих графиков более или менее просто интерпретируются. Тем не менее, здесь мы дадим интерпретацию нормального вероятностного графика, поскольку он наиболее часто используется при анализе справедливости предположений регрессии.

Как было замечено ранее, множественная линейная регрессия предполагает линейную связь между переменными в уравнении, и нормальным распределением остатков. Если эти предположения нарушаются, окончательные заключения могут оказаться неточными. Нормальный вероятностный график остатков наглядно показывает наличие или отсутствие больших отклонений от высказанных предположений. Нажмите кнопку Нормальный во вкладке Вероятностные графики для построения этого графика.

Этот график строится следующим образом. Сначала остатки регрессии ранжируются. Для этих упорядоченных остатков вычисляются z-значения (т.е. стандартные значения нормального распределения), исходя из предположения, что данные имеют нормальное распределение. Эти z-значения откладываются по оси Y на графике.

Если наблюдаемые остатки (отложенные по оси X) нормально распределены, то все значения будут располагаться на графике вблизи прямой линии; на данном графике все точки лежат очень близко к прямой линии. Если остатки не распределены нормально, то они будут отклоняться от линии. На этом графике также могут стать заметны выбросы.

Если имеющаяся модель плохо согласуется с данными, и данные на графике, похоже, образуют некоторую структуру (например, облако наблюдений принимает S-образную форму) около линии регрессии, то, возможно, будет полезным применение некоторого преобразования зависимой переменной (например, логарифмирование с целью «поджать» хвост распределения, и т.п.; см. также краткое обсуждение преобразований Бокса-Кокса и Бокса-Тидвелла в разделе Примечания и техническая информация). Обсуждение подобных методов лежит за рамками данного руководства. Однако слишком часто исследователи просто принимают свои данные, не пытаясь присмотреться к их структуре или проверить их на соответствие своим предположениям, что приводит к ошибочным заключениям. По этой причине одной из основных задач, стоявшей перед разработчиками пользовательского интерфейса модуля Множественной регрессии было максимально возможное упрощение (графического) анализа остатков.

Для изучения этого метода используем данные, показанные в табл.40.

В качестве оценки (О) студентов (Ст) на контрольной работе здесь использован процент правильных результатов по отношению к общему количеству заданий и вопросов. Если студент успешно выполнил все задания и правильно ответил на все вопросы, то его оценка О = 100%. В данной выборке (табл.40) таких студентов нет. Самый лучший результат здесь у студента №22, который успешно выполнил 93% всех заданий. А, например, студент №1 не справился ни с одним заданием и не ответил верно ни на один вопрос.

ПО – процент отсутствия. Если студент присутствовал в течение всего времени тренировочных занятий, то ПО = 0%. В данной выборке таких меньшинство. А, например, студенты №1 и №12 пропустили более половины времени, в течение которого можно было готовиться к контрольной работе.

Остальные переменные содержат субъективные оценки, выставленные преподавателями по шкалам семантического дифференциала.

Допустим, главной целью занятий является изучение компьютерной программы. Тогда мы сразу же, уже на первых занятиях, замечаем существенные различия между студентами в скорости и безошибочности работы. Обусловленные не тренировочными занятиями, а предшествующим опытом. Чем большее количество программ студент изучил ранее, чем проще ему разбираться с новой. Это приобретенный ранее опыт, имеющий непосредственное отношение к теме занятий, к содержанию контрольной работы.

Один человек всегда работает эффективнее другого. Даже если они раньше получили, казалось бы, один и тот же опыт. Дело не только в опыте, но также и в способностях, которые не являются результатом опыта в данной конкретной области. Но всегда ли мы можем отделить одно от другого? В какой степени успехи студента обусловлены предшествующим опытом в данной области, а в какой степени – соответствующими способностями? Чтобы не отвечать на такой сложный вопрос, эти составляющие сейчас (табл.40) просто объединены в одну переменную: Опыт и способности (ОС).

Для оценивания использована следующая шкала: полюс 1 – отсутствие опыта и/или слабые способности; полюс 7 – большой опыт и/или высокий уровень способностей. Если, например, три преподавателя поставили студенту соответственно оценки 6, 7, 6, то его средняя оценка приблизительно такова ОС = 6,3. В данной выборке это студенты №6, №13 и №24.

ДС – другие способности. Они, в отличие от ОС, не имеют никакого отношения к теме занятий и содержанию контрольной работы. Оценка 1 соответствует отсутствию каких-либо проявлений подобных талантов, а оценка 7 – наоборот, высокой степени их выраженности. Мы могли бы уточнить понятие ДС, например, назвать эти способности коммуникативными. Но для изучения регрессионного анализа это не принципиально. Важно здесь только лишь то, что они не влияют на оценку по данному предмету.

П – поведение на тренировочном занятии. Оценку 7 получают студенты, которые активно и внимательно разбираются с заданиями. Оценка 1 – наоборот, соответствует отсутствию каких-либо попыток выполнить задания и понять их смысл. Переменная М содержит информацию о мотивации: 1 – низкий уровень мотивации, 7 – высокий уровень мотивации.

Итак, назовем переменные еще раз:

Ст – студент;
О – оценка на контрольной работе;
ПО – процент отсутствия;
ОС – приобретенные ранее опыт и способности, обеспечивающие быстрое и правильное выполнение заданий;
ДС – другие способности (не помогающие в выполнении заданий);
П – поведение на тренировочных занятиях;
М – мотивация.

Надо сразу же заметить, что большинство переменных здесь не являются метрическими. Скорее их надо отнести к порядковым. Кроме того, это небольшая выборка и на нормальность распределения переменные не проверены. Следовательно, применение параметрических методов, в том числе и линейного регрессионного анализа, можно признать некорректным. Однако, это замечание является критичным только лишь при проведении реальных исследований. Если же наша цель заключается только в изучении SPSS, то эту проблему можно проигнорировать.

Коэффициенты корреляции Пирсона. Перед выполнением регрессионного анализа проанализируем вначале корреляционные связи между всеми 6-ю переменными (Analyze > Correlate > Bivariate). Ок.

Как и следовало ожидать, Оценка на контрольной работе связана здесь со всеми переменными кроме Других способностей. Связь Оценки с Опытом-Способностями несколько менее значима (p = 0,02) по сравнению с остальными тремя переменными (p 0,01). В большей степени повлияли на Оценку присутствие и активная работа на тренировочных занятиях. Причем, связь О*ПО является отрицательной, что и неудивительно: чем больше занятий пропустил студент, тем меньше знаний и навыков он получил, что и привело к снижению Оценки. Кроме того, выявлена очень сильная связь между Поведением и Мотивацией. Это понятно, ведь различия в Поведении здесь обусловлены, прежде всего, различиями в Мотивации.

Регрессионный анализ. Откройте меню Analyze > Regression и выберите линейную модель. В качестве зависимой (dependent) переменной используем Оценку, а в качестве независимых (independents) переменных – Процент отсутствия, Опыт-Способности, Другие способности и Поведение. Не будем пока что включать в анализ только Мотивацию. Номера студентов здесь будут являться обозначениями случаев (case labels). В диалоговом окне Statistics включите дополнительно диагностику коллинеарности и диагностику остатков (residuals) для всех (all) случаев (cases). Continue, Ok.

Мы здесь рассмотрим только лишь небольшую часть возможностей регрессионного анализа. Более полное описание, при необходимости, можете найти в текстовом файле «Другие результаты».

Квадрат (square) множественного коэффициента корреляции (R) свидетельствует о том, что модель объясняет приблизительно 86% дисперсии. Или 83%, если использовать уточненное (adjusted) значение. Согласно таблице ANOVA, статистическая значимость модели очень высока (p Таким образом, изучаемые нами данные (табл.40) можно описать следующим уравнением:

О = 0,46 – 0,63•ПО + 4,8•ОС + 0,5•ДС + 7,5•П

Поскольку модель в целом высоко значима и объясняет достаточно большую долю дисперсии, это уравнение можно использовать для прогнозов. Подставьте в него наблюдаемые значения независимых переменных и получите ожидаемое значение зависимой переменной. Нестандартизованные коэффициенты интерпретируются легко. Коэффициент B представляет среднее изменение зависимой переменной при изменении на единицу соответствующей этому коэффициенту независимой переменной при неизменных других независимых переменных. Но близость коэффициентов B еще не свидетельствует о приблизительно равных вкладах соответствующих независимых переменных. Мы видим, например, что абсолютные значения коэффициентов для Процента отсутствия (0,63) и Других способностей (0,5) близки. Но сравнение шкал этих переменных: 0…100 и 1…7 позволяет понять, что переменная Процент отсутствия вносит в дисперсию зависимой переменной гораздо больший вклад.

Непосредственно сравнивать вклады независимых переменных позволяют стандартизованные коэффициенты регрессии Beta. Стандартизация здесь означает умножение коэффициента B на стандартное отклонение независимой переменной и его деление на стандартное отклонение зависимой переменной. Сравним независимые переменные: наибольший вклад вносит Поведение на тренировочном занятии (Beta=0,62), несколько меньший вклад вносит Процент отсутствия (Beta= – 0,46) и т.д. Заметьте, что уровни значимости Sig здесь менее удобны: если не пытаться выяснять их более точные значения, то можно сделать вывод, что все независимые переменные кроме Других способностей вносят одинаково большой вклад (p Но большинство из них можно свести к следующим:

1) повлияли факторы, не учтенные в модели;
2) измерения по некоторым переменным выполнены неточно;
3) линейная модель неспособна точно описать закономерность, наблюдающуюся в данных.

Мультиколлинеарность. Сильная связь между независимыми переменными может настолько искажать результаты регрессионного анализа, что доверять этим результатам уже невозможно. Просмотрите вычисленные ранее коэффициенты корреляции: сильных и значимых связей между переменными ПО, ОС, ДС, П не выявлено. Следовательно, проблем с мультиколлинеарностью здесь быть не может. Чтобы подтвердить это, необходимо убедиться, что показатели Condition index в таблице Collinearity diagnostics не превышают значение 15. Так оно и есть.

Теперь давайте убедимся, что может быть и иначе. Выполните регрессионный анализ еще раз, но теперь дополнительно добавьте в список независимых переменных переменную Мотивация. Теперь в модели будет 5 независимых переменных. Все остальные настройки диалоговых окон оставьте прежними. Ок.

Сравните результаты с предыдущими. Объясняемый моделью процент дисперсии изменился несущественно. В соответствии с коэффициентом детерминации (R square) он слегка повысился, однако в соответствии с уточненным (adjusted) коэффициентом – наоборот, слегка понизился. Модель в целом по-прежнему высоко статистически значима.

Просмотрите снова вычисленные ранее коэффициенты корреляции: Оценка сильно положительно связана и с Поведением и с Мотивацией. Но еще более сильно Поведение и Мотивация связаны между собой. Поскольку сейчас в модели обе эти переменные используются в качестве независимых, то сильная связь между ними должна настораживать. Убедитесь, что это действительно не лучшим образом повлияло на результаты (таблица coefficients). Во-первых, вклад Мотивации оказался отрицательным (B = -3,9). Во-вторых, вклад Поведения и Мотивации оказался статистически незначимым (p = 0,088 и p = 0,561). Как это понять? Ведь это полностью противоречит результатам, полученным ранее: Оценка значимо (p

Регрессионный анализ является одним из наиболее распространённых методов обработки экспериментальных данных при изучении зависимостей в физике, биологии, экономике, технике и других областях.

Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. Регрессионный анализ заключается в определении аналитического выражения, в котором изменение одной величины (называемой зависимой или результативным признаком) y обусловлено влиянием одной или нескольких независимых величин (факторов) x1, x2,…, xn, а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения.

Регрессия может быть однофакторной (парной) и многофакторной (множественной). Для простой (парной) регрессии в условиях, когда достаточно полно установлены причинно-следственные связи, можно использовать графическое изображение. При множественности причинных связей невозможно чётко разграничить одни причинные явления от других. В этом случае наиболее приемлемым способом определения зависимости (уравнения регрессии) является метод перебора различных уравнений, реализуемый с помощью компьютера.

После выбора вида регрессионной модели, используя результаты наблюдений зависимой переменной и факторов, нужно вычислить оценки (приближённые значения) параметров регрессии, а затем проверить значимость и адекватность модели результатам наблюдений.

Порядок проведения регрессионного анализа следующий:

• выбор модели регрессии, что заключает в себе предположение о зависимости функций регрессии от факторов;
• оценка параметров регрессии в выбранной модели методом наименьших квадратов;
• проверка статистических гипотез о регрессии.

Построим приближённую зависимость времени простоя техники от времени работы и месяца. На существование этой зависимости, причём линейной, указывает корреляционный анализ. Имея зависимость, выраженную в виде формулы, можно прогнозировать время простоя на следующий период и оценить недополученную прибыль в результате простоев, что так любят делать экономисты.

Линейный регрессионный анализ выполняется в модуле Statistics/ MultipleRegression. В стартовом диалоговом окне этого модуля при помощи кнопки Variables указываются зависимая (dependent) и независимые (independent) переменные.

В поле Inputfileуказывается тип файла с данными:

RawData – данные в виде строчной таблицы (по умолчанию);
CorrelationMatrix – данные в виде корреляционной матрицы.

В стартовом окне можно задать и дополнительные опции и параметры анализа. Например, можно выбрать определенное подмножество наблюдений для анализа или приписать вес переменным. Также можно задать и опции, которые относятся непосредственно к статистической процедуре: задать правило обработки пропущенных данных, выбрать метод анализа по умолчанию и др.

Для вывода результатов и их анализа нажмите на кнопку ОК. Система произведет вычисления, и на экране появится окно результатов. Оно имеет простую структуру: верхняя часть окна – информационная, нижняя содержит функциональные кнопки, позволяющие всесторонне просмотреть результаты анализа.

Dependent – имя зависимой переменной. В нашем случае это «Простой».

No. of cases – число наблюдений, по которым построена регрессия. В примере число равно 12.

Multiple R – коэффициент множественной корреляции. Эта статистика полезна в множественной регрессии, когда вы хотите описать зависимости между переменными. Она может принимать значения от 0 до 1 и характеризует тесноту линейной связи между зависимой и всеми независимыми переменными.

R – квадрат коэффициента множественной корреляции (R2), называемый коэффициентом детерминации.

Коэффициент детерминации является одной из основных статистик в данном окне, он показывает долю общего разброса (относительно выборочного среднего зависимой переменной), которая объясняется построенной регрессией. Чем ближе коэффициент детерминации к единице, тем качественнее найдена модель (объясняет поведение большего числа точек).

Коэффициент детерминации обладает существенным недостатком. При равенстве числа независимых переменных q числу наблюдений n величина R2 равна 1. По мере добавления переменных в уравнение значение R2 неизбежно возрастает. Это ведет к неоправданному предпочтению моделей с большим числом независимых переменных. Отсюда следует, что необходима поправка к R2, которая бы учитывала число переменных и наблюдений. В результате получаем скорректированный коэффициент детерминации (adjusted R).

Включение новой переменной в регрессионное уравнение увеличивает R2 не всегда, а только в том случае, когда частный F-критерий при проверке гипотезы о значимости включаемой переменной больше или равен 1. В противном случае включение новой переменной уменьшает значение коэффициентов детерминации. Таким образом, скорректированный R2 можно с большим успехом (по сравнению с R2) применять для выбора наилучшего подмножества независимых переменных в регрессионном уравнении.

F-критерий используется для оценки адекватности регрессионной модели, определяет отношение дисперсии оценки модели к дисперсии остатка.

Standard Error of estimate – стандартная ошибка оценки. Эта статистика является мерой рассеяния наблюдаемых значений относительно регрессионной прямой.

Intercept – оценка свободного члена регрессии. Значение коэффициента b0 в уравнении регрессии.

Std. Error – стандартная ошибка оценки свободного члена. Стандартная ошибка коэффициента b0 в уравнении регрессии.

F – значения F-критерия для проверки гипотезы b1=0.
df – число степеней свободы F-критерия.
p – уровень значимости.
t–t-критерий для проверки гипотезы о равенстве нулю свободного члена уравнения. Если p больше заданного уровня значимости Alpha, то гипотеза b0=0 принимается.
Beta – коэффициенты b уравнения.

В информационной части прежде всего нужно смотреть на значение коэффициента детерминации. В нашем примере он равен 0,988. Это значит, что построенная регрессия объясняет 98,8 % разброса значений переменной «Простой» относительно среднего. Это хороший результат.

Далее смотрим на значение F-критерия и уровень его значимости p. F-критерий используется для проверки гипотезы, утверждающей, что между зависимой переменной «Простой» и независимой переменной «Работа» нет линейной зависимости, т.е. b1=0, против альтернативы «b1 не равен нулю». В данном примере большое значение F-критерия 373,3964 и даваемый в окне уровень значимости p=0,0112 показывают, что построенная регрессия значима.

При помощи кнопок диалогового окна Multiple Regressions Results результаты регрессионного анализа можно просмотреть более детально. Щёлкните далее на кнопку Summary:Regression rezults (краткие результаты регрессии).

Во втором столбце таблицы (Beta) выводятся стандартизованные коэффициенты регрессии, в третьем (Std.Err. of Beta) – их стандартные отклонения. В случае множественной регрессии стандартизованные коэффициенты регрессии используются для сравнения влияния на зависимую переменную факторов, имеющих различную размерность.

В четвёртом столбце таблицы имеются оценки неизвестных параметров модели:

b0 = –705,680;
b1 = 51,152;
b2 = 0,479;
в пятом столбце (St.Err. of B) – их стандартные отклонения.

Итак, искомая модель зависимости времени простоя техники от времени работы и месяца имеет вид:

Простой = –705,680+51,152*Месяц+ 0,479*Работа

Из модели очевидна необходимость снижения сезонности работ.

В шестом и седьмом столбцах таблицы выводятся t-статистики и соответствующие уровни значимости для проверки гипотезы о равенстве нулю коэффициентов регрессии. Для нашего примера гипотеза для b0 и b2 отклоняется.

Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.

Вид множественной линейной модели регрессионного анализа:

Y = b0 + b1xi1 + . + bjxij + . + bkxik + ei

где ei — случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.

Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой переменной.

Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом.

Матричная запись множественной линейной модели регрессионного анализа:

где Y — случайный вектор — столбец размерности (n x 1) наблюдаемых значений результативного признака (y1, y2. yn);
X — матрица размерности [n x (k+1)] наблюдаемых значений аргументов;
b — вектор — столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели;
e — случайный вектор — столбец размерности (n x 1) ошибок наблюдений (остатков).

На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, что эти данные являются значениями случайной величины. Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).

Пример функциональной зависимости выпуск продукции и ее потребление в условиях дефицита.

Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов образование, здоровье и т.д. эта зависимость может быть искажена.

Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом (от лат. correlatio соотношение, соответствие).

Основная задача корреляционного анализа это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов. Характер связи между показателями определяется по корреляционному полю. Если у зависимый признак, а х независимый, то, отметив каждый случай х (i) с координатами х и yi, получим корреляционное поле.

Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы.

Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от – 0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полном ее отсутствии.

Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.

Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна. Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

По числу факторов различают одно-, двух- и многофакторные уравнения регрессии.

По характеру связи однофакторные уравнения регрессии подразделяются:

a. на линейные:
У= a*bx ,
где х экзогенная (независимая) переменная, у эндогенная (зависимая, результативная) переменная, а,b параметры;
b. степенные:
У= a*
c. показательные
У= a*

Задача №2. Основы регрессионного анализа

1. Определить уравнение связи между производительностью труда и рентабельностью предприятия. Вычислить коэффициент корреляции между производительностью труда и рентабельностью предприятия. Проверить гипотезу о значимости отличия коэффициента корреляции от нуля.

Считая связь между производительностью труда и рентабельностью линейной, построить уравнения связи между названными показателями, используя метод наименьших квадратов. Проверить гипотезу об отличии от нуля коэффициента регрессии. Дать экономическую интерпретацию полученных результатов.

2. Предположить, что связь между производительностью труда и рентабельностью, например, степенная, показательная или др. Произвести все расчеты. Выбрать ту функциональную зависимость, где ошибка коэффициента регрессии Sa1 наименьшая.

источник